基于時間序列模型的變電站沉降預測分析

　　摘要：變形分析與預報是變形監測數據處理的重要內容，而時間序列模型是常用的變形分析與預報工具。本文采用時間序列模型對變電站沉降數據進行分析建模，從而掌握變電站的沉降規律，預測未來沉降趨勢，對下一步施工具有實際指導意義。

　　本文源自.測繪與空間地理信息,2019,42(12):206-207+210.《測繪與空間地理信息》(月刊)創刊于1978年，由黑龍江省測繪學會主辦。反映測繪學科及地理空間信息科學前沿理論和技術并指導地理信息工作者從事科研、開發、生產的技術性、知識性刊物，主要刊載測繪高新技術、地球空間信息和地理信息系統的前沿理論與技術;地理信息系統工程建設的技術總結與經驗交流;測繪行業管理與改革的先進經驗;測繪生產技術交流、科研成果推廣及教學經驗介紹等;測繪學和地理信息學中的理論探討;國內外地理信息學術動態及測繪科技報道與介紹;測繪科普知識;測繪儀器新發展等。榮獲連續多年獲中國測繪協會期刊獎。

　　變電站在施工過程中不可避免地會發生沉降變形，當變形量超過一定的范圍時可能會引發災害，威脅人身安全，給國民經濟造成損失。因此，需要對變形監測數據進行科學的分析處理，識別變形特征，發現和掌握變形規律，并做出科學預報。時間序列模型是一種成熟的數據處理方法，已廣泛應用于氣象、水文、經濟、電力等領域[1,2]。本文基于時間序列模型，分析研究了某變電站沉降監測數據的變形規律，建立了沉降數據的時間序列模型，并對未來的變形趨勢進行預測，準確率較高，具有較強的現實意義。

　　1、時序模型簡介

　　時間序列分析的基本思想是將數據序列看作隨時間t變化的隨機變量，即使此序列中單個數據構成的序列值不確定，但整個序列會呈現出一定的變化規律，從而用數學模型去近似模擬表現出來。具體來說，對于平穩、正態、零均值的時間序列{xt}，xt的值不僅與前n步的值xt-1,xt-2，…，xt-n有關，而且還與前m步的隨機干擾項ut-1,ut-2，…，ut-m有關(n,m=1,2，…)。

　　時間序列的基本模型有3種[3]:自回歸模型、移動平均模型和自回歸移動平均模型。

　　1.1自回歸模型

　　上式是p階自回歸模型，表示成AR(p)。式中，p是模型的階數;φ1，φ2，…，φp為自回歸系數;ut是白噪聲，且ut～N(0，σu2)。

　　AR(p)模型要求隨機干擾項{ut}相互獨立，且與觀測值{xt}不相關。同時要求用AR(p)模型對序列{xt}擬合后的殘差序列必須是白噪聲。

　　1.2移動平均模型

　　式(2)稱為移動平均模型，記為MA(q)，式中，q為模型階數，θ1，θ2，…，θ3為移動平均系數;{ut}是白噪聲序列，且ut:N(0，σu2)。

　　MA(q)模型是用過去各期隨機干擾(預測誤差)的線性組合來表示當前預測值。

　　1.3自回歸移動平均模型

　　自回歸移動平均模型同時包含自回歸和移動平均兩部分，表達式如下[4]:

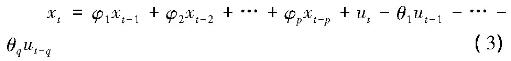
　　記為ARMA(p,q)，式中，p和φi(i=1,2，…，p)分別是自回歸階數和系數，q和θi(i=1,2，…，p)分別是移動平均的階數和系數。

　　2、數據處理

　　2.1數據來源

　　本文數據來自某1000kV交流特高壓交流輸變電工程沉降監測項目。該工程共觀測了127個沉降點，均勻分布于變電站主要建筑物的基礎受力點上。本文選取其中一個點自2015年2月13日至2016年6月18日期間共計23期的沉降監測數據。

　　2.2數據預處理

　　時間序列建模要求樣本數據是平穩、正態、零均值的時間序列，所以在建模之前要對數據進行平穩性檢驗，對不符合要求的序列要進行平穩化處理。

　　時間序列平穩性檢驗的方法主要有兩種:圖檢驗法和單位根檢驗法。由于圖檢驗法帶有很強的主觀性，當圖檢驗法不能明確得出結論時，就需要通過確定的準則來判斷平穩性，通常是通過單位根檢驗統計量來對序列平穩性進行假設檢驗。單位根檢驗是對自回歸特征方程的特征根進行檢驗，通過驗證特征根的模是否都大于1來判斷是否平穩。ADF檢驗統計量，又稱增廣DF檢驗(AugmentedDikey-Fuller)，是單位根檢驗中最常用的統計量，通過檢驗自回歸系數之和是否小于1來判斷該序列是否平穩，令ρ=φ1+φ2+…+φp-1，則原假設H0:ρ≥0(序列非平穩)，ADF檢驗統計量:

　　式中，S(ρ)是參數ρ的樣本標準差。

　　對h序列進行ADF單位根檢驗:假設h序列存在ADF單位根，計算得出t統計量的p值為0.8619，遠超出顯著性水平0.05，因此假設成立，h序列不平穩，進行一階差分得到Dh。然后對Dh進行ADF檢驗，t統計量的p值為0.0298，低于0.05，故Dh序列平穩。

　　2.3模型識別與參數估計

　　自相關函數和偏自相關函數是識別ARMA模型的最主要工具，若樣本自協方差函數(ACF)在q步截尾，則判定xt是MA(q)序列;若樣本偏自相關函數(PACF)在p步截尾，則判定xt是AR(p)序列;若兩者都不截尾，而僅是依負指數衰減，這時可初步認為xt是ARMA序列，它的階需要從低階到高階逐步增加，再通過檢驗來確定，一般使用AIC準則進行定階，即在p,q的一定變化范圍內，尋求使得AIC(S)最小的(^p,^q)作為(p,q)的估計值。

　　從圖1可以看出，ACF和PACF都不截尾，給定(p,q)上限，一般取樣本長度(L)的L/10或lnL，這里取上限為3，經檢驗，當p=3,q=2時AIC值最小，所以最終的模型定為ARMA(3,2)。根據最小二乘準則確定模型的參數如下:

　　圖1一階差分序列的自相關和偏相關系數圖

　　2.4模型預測與檢驗

　　對原始數據序列前20個數據的擬合結果如圖2所示。

　　圖2擬合效果圖

　　參數估計之后，要對模型的適用性進行檢驗，本質上也是對模型殘差序列進行白噪聲檢驗。若殘差序列是白噪聲，則說明建立的模型已經包含了原始時間序列的所有趨勢，可以進行預測;否則說明還有一些重要信息沒被提取，應重新進行模型識別和定階。

　　對殘差序列進行自相關分析和ADF單位根檢驗，如圖3所示，該序列的ACF和PACF除了第一階外，其余都落在臨界值以內。而且t檢驗統計量的p值為0.013<0.05，拒絕原假設，不存在單位根。所以，可以判定殘差序列是白噪聲序列，也說明用ARMA(3,2)模型對該數據序列建模是有效的。

　　圖3殘差的自相關和偏相關系數圖

　　2.5模型預測

　　對原始數據序列用ARMA(3,2)模型進行擬合和預測，限于篇幅，本文僅展示部分數據的擬合結果。從圖2及表1、表2可以看出，沉降數據的擬合和預測效果都比較好，兩者的相對平均誤差分別為2.3%和2.5%。說明對于該變電站沉降時間序列，采用ARMA(3,2)模型進行建模可以較為準確地反映變電站的沉降變形規律，并且能夠以較高的精度進行短期預測。

　　表1沉降數據的部分擬合結果(單位:mm)

　　表2沉降數據的預測結果(單位:mm)

　　3、結束語

　　變電站的沉降監測是電力工程勘測中的重要內容，對沉降數據的變形分析和預報必不可少。本文采用時間序列模型對某變電站工程的沉降數據序列建模，然后進行預測分析，結果表明:ARMA模型能夠較為準確地反映變電站沉降規律，并且能以較高的精度對變電站沉降進行預測，取得了較好的效果。

　　參考文獻：

　　[1]劉大杰,陶本藻.實用測量數據處理方法[M].北京:測繪出版社,2000.

　　[2]楊位欽,顧嵐.時間序列分析與動態數據建模[M].北京:北京工業學院出版社,1986.

　　[3]潘國榮.基于時間序列分析的動態變形預測模型研究[J].武漢大學學報,2005,30(6):483-487.

　　[4]史玉峰,孫保琪.時間序列分析及其在變形數據分析中的應用[J].金屬礦山,2004(8):13-15.